One to One Functions - Graph, Examples | Horizontal Line Test
What is a One to One Function?
A one-to-one function is a mathematical function where each input corresponds to a single output. In other words, for every x, there is just one y and vice versa. This signifies that the graph of a one-to-one function will never intersect.
The input value in a one-to-one function is the domain of the function, and the output value is the range of the function.
Let's study the examples below:
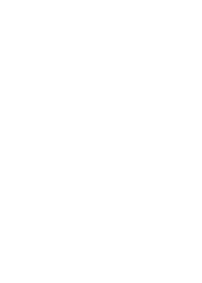
For f(x), every value in the left circle correlates to a unique value in the right circle. In the same manner, each value on the right side corresponds to a unique value in the left circle. In mathematical jargon, this implies every domain has a unique range, and every range owns a unique domain. Hence, this is a representation of a one-to-one function.
Here are some additional examples of one-to-one functions:
-
f(x) = x + 1
-
f(x) = 2x
Now let's look at the second example, which exhibits the values for g(x).
Pay attention to the fact that the inputs in the left circle (domain) do not have unique outputs in the right circle (range). Case in point, the inputs -2 and 2 have the same output, in other words, 4. In conjunction, the inputs -4 and 4 have identical output, i.e., 16. We can comprehend that there are matching Y values for multiple X values. Hence, this is not a one-to-one function.
Here are different examples of non one-to-one functions:
-
f(x) = x^2
-
f(x)=(x+2)^2
What are the properties of One to One Functions?
One-to-one functions have the following properties:
-
The function has an inverse.
-
The graph of the function is a line that does not intersect itself.
-
The function passes the horizontal line test.
-
The graph of a function and its inverse are identical regarding the line y = x.
How to Graph a One to One Function
In order to graph a one-to-one function, you are required to determine the domain and range for the function. Let's look at an easy representation of a function f(x) = x + 1.
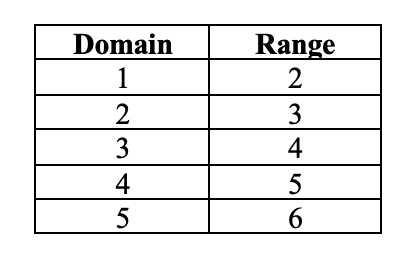
Once you have the domain and the range for the function, you have to chart the domain values on the X-axis and range values on the Y-axis.
How can you tell whether or not a Function is One to One?
To indicate whether a function is one-to-one, we can apply the horizontal line test. As soon as you graph the graph of a function, trace horizontal lines over the graph. If a horizontal line intersects the graph of the function at more than one point, then the function is not one-to-one.
Because the graph of every linear function is a straight line, and a horizontal line does not intersect the graph at more than one point, we can also reason that all linear functions are one-to-one functions. Keep in mind that we do not leverage the vertical line test for one-to-one functions.
Let's study the graph for f(x) = x + 1. Immediately after you graph the values for the x-coordinates and y-coordinates, you need to consider whether a horizontal line intersects the graph at more than one point. In this case, the graph does not intersect any horizontal line more than once. This signifies that the function is a one-to-one function.
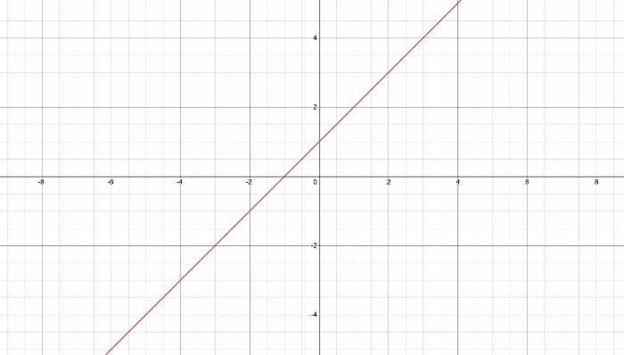
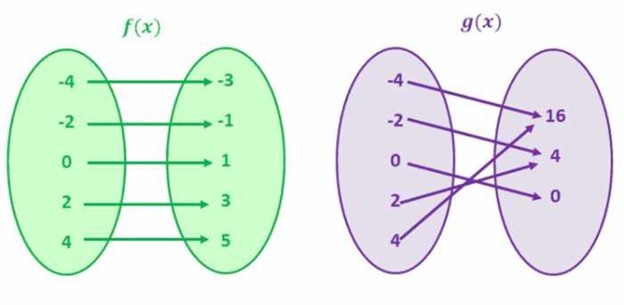
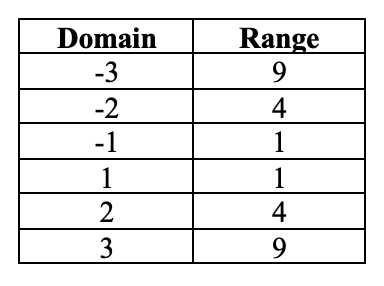
On the contrary, if the function is not a one-to-one function, it will intersect the same horizontal line multiple times. Let's look at the figure for the f(y) = y^2. Here are the domain and the range values for the function:
Here is the graph for the function:
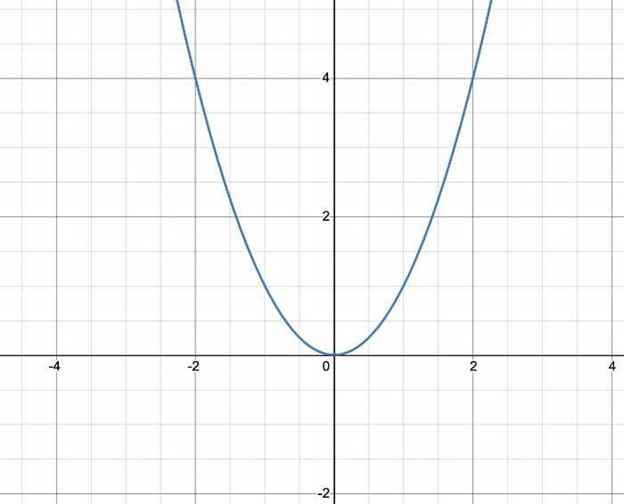
In this example, the graph meets numerous horizontal lines. For instance, for both domains -1 and 1, the range is 1. In the same manner, for either -2 and 2, the range is 4. This signifies that f(x) = x^2 is not a one-to-one function.
What is the inverse of a One-to-One Function?
Since a one-to-one function has a single input value for each output value, the inverse of a one-to-one function also happens to be a one-to-one function. The inverse of the function essentially undoes the function.
For Instance, in the example of f(x) = x + 1, we add 1 to each value of x in order to get the output, or y. The opposite of this function will subtract 1 from each value of y.
The inverse of the function is denoted as f−1.
What are the qualities of the inverse of a One to One Function?
The characteristics of an inverse one-to-one function are no different than all other one-to-one functions. This means that the opposite of a one-to-one function will hold one domain for every range and pass the horizontal line test.
How do you find the inverse of a One-to-One Function?
Figuring out the inverse of a function is simple. You simply have to switch the x and y values. For example, the inverse of the function f(x) = x + 5 is f-1(x) = x - 5.
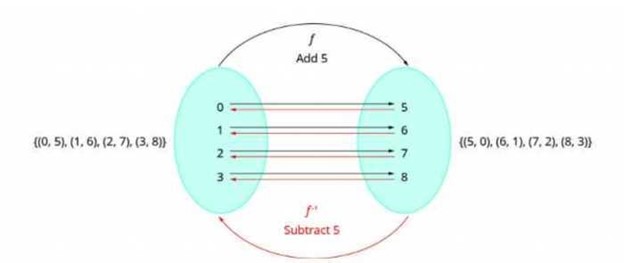
As we discussed earlier, the inverse of a one-to-one function reverses the function. Considering the original output value showed us we needed to add 5 to each input value, the new output value will require us to subtract 5 from each input value.
One to One Function Practice Examples
Consider the subsequent functions:
-
f(x) = x + 1
-
f(x) = 2x
-
f(x) = x2
-
f(x) = 3x - 2
-
f(x) = |x|
-
g(x) = 2x + 1
-
h(x) = x/2 - 1
-
j(x) = √x
-
k(x) = (x + 2)/(x - 2)
-
l(x) = 3√x
-
m(x) = 5 - x
For each of these functions:
1. Figure out whether or not the function is one-to-one.
2. Chart the function and its inverse.
3. Figure out the inverse of the function algebraically.
4. Specify the domain and range of every function and its inverse.
5. Use the inverse to find the solution for x in each calculation.
Grade Potential Can Help You Learn You Functions
If you are facing difficulties trying to understand one-to-one functions or similar concepts, Grade Potential can put you in contact with a 1:1 instructor who can support you. Our Centennial math tutors are experienced educators who support students just like you advance their skills of these subjects.
With Grade Potential, you can study at your own pace from the convenience of your own home. Schedule an appointment with Grade Potential today by calling (303) 578-1372 to learn more about our educational services. One of our team members will call you to better inquire about your requirements to set you up with the best instructor for you!